Question 1.
Using appropriate properties find:
(i) -2/5 x 3/5 + 5/2 - 3/5 x 1/6
(ii) 2/5 x (-3/7) - 1/6 x 3/2 + 1/14 x 2/5
Solution.
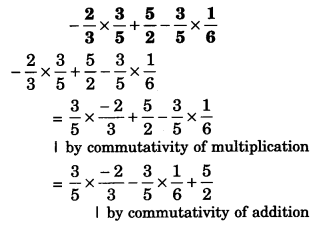
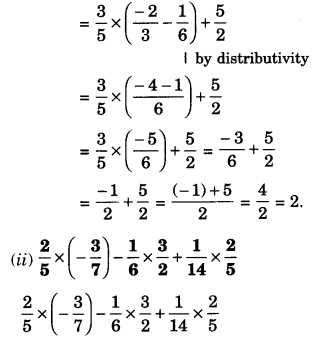

Question 2.
Write the additive inverse of each of the following:
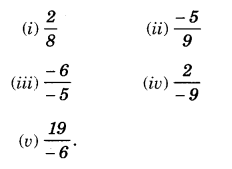
Solution.


Question 3.
Verify that - (-x) = x for :
(i) x=11/15
(ii)x=-13/17
Solution
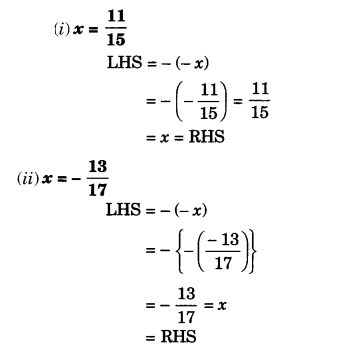
Question 4.
Find the multiplicative inverse of the following:
- (i)-13
- (ii) -13/19
- (iii) 1/5
- (iv) -5/8 x -3/7
- (v) -1 x -2/5
- (vi) -1
Solution.

Question 5.
Name the property under multiplication used in each of the following:
- (i)-4/5 x (1)=1 x -4/5= - 4/5
- (ii) - 13/17 x -2/7 = -2/7 x -13/17
- (iii) -19/29 x 29/-19 = 1
Solution.
- (i) 1 is the multiplicative identity
- (ii) Commutativity of multiplication
- (iii) Multiplicative inverse.
Question 6.
Multiply 6/13 by the reciprocal of -7/16
Solution.
Reciprocal of -7/16 is -1/67
Now,
6/13×-16/7=6×(-16)/13×7=-96/91
Question 7.
Tell what property allows you to compute : 1/3×(6×4/3) as (1/3×6)×4/3
Solution.
Associativity.
Question 8.
Is the 89 multiplicative inverse of -1 1/8 ? Why or why not?
Solution.
-1 1/8=-9/8
Now, 8/9×-9/8=-1=1
So, No ; 8/9 is not the multiplicative inverse of -1 1/8(=-9/8) because the product of 8/9 and -13(-) and -1 1/8(=-9/8) is not 1.
Question 9.
Is 0.3 the multiplicative inverse of 313 ? Why or why not?
Solution.
Yes ; 0.3 is the multiplicative inverse of 10/3 because
3/10×10/3=3×10/10×3=30/30=1
Question 10.
Write :
- (i) The rational number that does not have a reciprocal.
- (ii) The rational numbers that are equal to their reciprocals.
- (iii) The rational number that is equal to its negative.
Solution.
- (i) The rational number "0" does not have a reciprocal.
- (ii) The rational numbers 1 and (-1) are equal to their own reciprocals.
- (iii) The rational number 0 is equal to its negative.
Question 11.
Fill in the blanks :
- (i) Zero has....reciprocal.
- (ii) The numbers....and...are their own reciprocals.
- (iii) The reciprocal of - 5 is......
- (iv) Reciprocal of 1x, where x?0
- (v) The product of two rational numbers is always a....
- (vi) The reciprocal of a positive rational number is....
Solution.
- (i) Zero has no reciprocal.
- (ii) The numbers 1 and -1 are their own reciprocals.
- (iii) The reciprocal of - 5 is ?15
- (iv) Reciprocal of 1x, where x?0 is x.
- (v) The product of two rational numbers is always a rational number.
- (vi) The reciprocal of a positive rational number is positive.