NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1.

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1

Ex 4.1 Class 9 Maths Question 1.

The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
(Take the cost of a notebook to be Rs. x and that of a pen to be Rs.y).
Solution:
Let the cost of a notebook = Rs. x
and the cost of a pen = Rs. y
According to the condition, we have
[Cost of a notebook] =2 x [Cost of a pen]
i. e, (x) = 2 x (y) or, x = 2y
or, x - 2y = 0
Thus, the required linear equation is x - 2y = 0.

Ex 4.1 Class 9 Maths Question 2.

Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

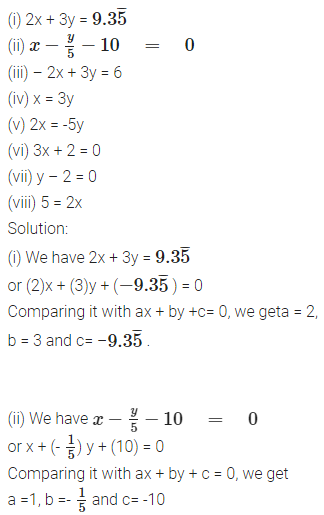
(iii) Wehave -2x + 3y = 6 or (-2)x + (3)y + (-6) = 0
Comparing it with ax - 4 - by + c = 0,we get a = -2, b = 3 and c = -6.

(iv) We have x = 3y or (1)x + (-3)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 1, b = -3 and c = 0.
(v) We have 2x = -5y or (2)x + (5)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 2, b = 5 and c = 0.
(vi) We have 3x + 2 = 0 or (3)x + (0)y + (2) = 0 Comparing it with ax + by + c = 0, we get a = 3, b = 0 and c = 2.
(vii) We have y - 2 = 0 or (0)x + (1)y + (-2) = 0 Comparing it with ax + by + c = 0, we get a = 0, b = 1 and c = -2.
(viii) We have 5 = 2x ? 5 - 2x = 0
or -2x + 0y + 5 = 0
or (-2)x + (0)y + (5) = 0
Comparing it with ax + by + c = 0, we get a = -2, b = 0 and c = 5.

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.2

Ex 4.2 Class 9 Maths Question 1.

Which one of the following options is true, and why?
y = 3x + 5 has
(i) a unique solution,
(ii) only two solutions,
(iii) infinitely many solutions
Solution:
Option (iii) is true because for every value of x, we get a corresponding value of y and vice-versa in the given equation.
Hence, given linear equation has an infinitely many solutions.

Ex 4.2 Class 9 Maths Question 2.

Write four solutions for each of the following equations:
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
Solution:
(i) 2x + y = 7
When x = 0, 2(0) + y = 7 ⇒ y = 7
∴ Solution is (0, 7)
When x =1, 2(1) + y = 7 ⇒ y = 7 - 2 ⇒ y = 5
∴ Solution is (1, 5)
When x = 2, 2(2) + y =7y = 7 - 4 ⇒ y = 3
∴ Solution is (2, 3)
When x = 3, 2(3) + y = 7y = 7 - 6 ⇒ y = 1
∴ Solution is (3, 1).

(ii) πx + y = 9
When x = 0, π(0) + y = 9 ⇒ y = 9 - 0 ⇒ y = 9
∴ Solution is (0, 9)
When x = 1, π(1) + y = 9 ⇒ y = 9 - π
∴ Solution is (1, (9 - π))
When x = 2, π(2) + y = 9 ⇒ y = 9 - 2π
∴ Solution is (2, (9 - 2π))
When x = -1,π(-1) + y = 9 ⇒ y = 9 + π
∴ Solution is (-1, (9 + π))

(iii) x = 4y
When x = 0, 4y = 1 ⇒ y = 0
∴ Solution is (0, 0)
When x = 1, 4y = 1 ⇒ y = 1/4
∴ Solution is (1,1/4)
When x = 4, 4y = 4 ⇒ y = 1
∴ Solution is (4, 1)
When x = 4, 4y = 4 ⇒ y = -1
∴ Solution is (-4, -1)

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.3

Ex 4.3 Class 9 Maths Question 1.

Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
Solution:
(i) x + y = 4 ? y = 4 – x
If we have x = 0, then y = 4 – 0 = 4
x = 1, then y =4 – 1 = 3
x = 2, then y = 4 – 2 = 2
∴ We get the following table:

Plot the ordered pairs (0, 4), (1,3) and (2,2) on the graph paper. Joining these points, we get a straight line AB as shown.

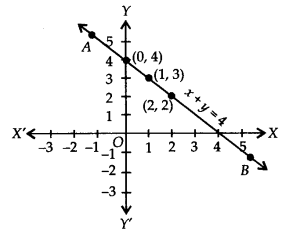
Thus, the line AB is the required graph of x + y = 4

(ii) x – y = 2 ? y = x – 2
If we have x = 0, then y = 0 – 2 = -2
x = 1, then y = 1 – 2 = -1
x = 2, then y = 2 – 2 = 0
∴ We get the following table:

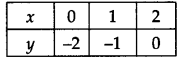
Plot the ordered pairs (0, -2), (1, -1) and (2, 0) on the graph paper. Joining these points, we get a straight line PQ as shown.

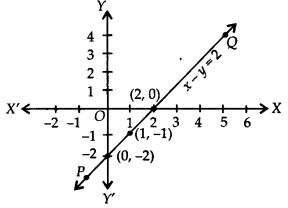
Thus, the ime is the required graph of x – y = 2

(iii) y = 3x
If we have x = 0,
then y = 3(0) ⇒ y = 0
x = 1, then y = 3(1) = 3
x= -1, then y = 3(-1) = -3

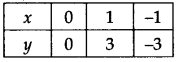
Plot the ordered pairs (0, 0), (1, 3) and (-1, -3) on the graph paper. Joining these points, we get a straight line LM as shown.

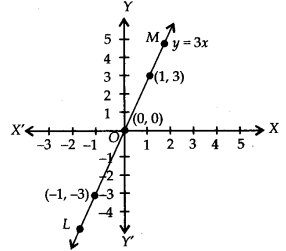
Thus, the line LM is the required graph of y = 3x.

(iv) 3 = 2x + y ⇒ y = 3 - 2x
If we have x = 0, then y = 3 - 2(0) = 3
x = 1,then y = 3 - 2(1) = 3 - 2 = 1
x = 2,then y = 3 - 2(2) = 3 - 4 = -1
∴ We get the following table:

Plot the ordered pairs (0, 3), (1, 1) and (2, – 1) on the graph paper. Joining these points, we get a straight line CD as shown.

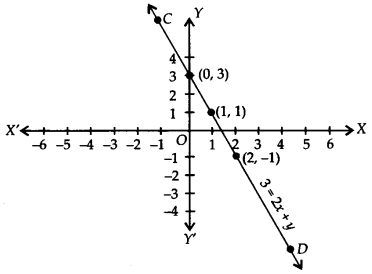
Thus, the line CD is the required graph of 3 = 2x + y.

Ex 4.3 Class 9 Maths Question 2.

Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
Solution:
(2, 14) means x = 2 and y = 14
Equations which have (2,14) as the solution are (i) x + y = 16, (ii) 7x – y = 0
There are infinite number of lines which passes through the point (2, 14), because infinite number of lines can be drawn through a point.

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.4

Ex 4.4 Class 9 Maths Question 1.

Give the geometric representations of y = 3 as an equation
(i) in one variable
(ii) in two variables
Solution:
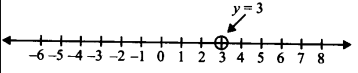
(i) y = 3
∴ y = 3 is an equation in one variable, i.e., y only.
∴ y = 3 is a unique solution on the number line as shown below:

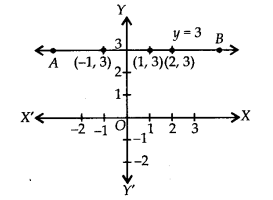
(ii) y = 3
We can write y = 3 in two variables as 0.x + y = 3
Now, when x = 1, y = 3
x = 2, y = 3
x = -1, y = 3
∴ We get the following table:

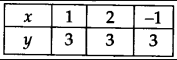
Plotting the ordered pairs (1, 3), (2, 3) and (-1, 3) on a graph paper and joining them, we get aline AB as solution of 0. x + y = 3,
i.e. y = 3.

Post your comments

Your mobile number will not be published.

View Comments

• Sagar singh
• 2022-March-22 18:00:44

I want glossary PDF

• Anuradha Rawat
• 2021-September-18 08:27:43

Very much composed answers

• Mayank
• 2021-March-26 11:24:00

Ok

• Ramu
• 2020-May-05 15:49:15

NCERT Solutions For Class 11