NCERT CBSE for Class 10 Maths Chapter 1 Real Numbers Important Questions
Real Numbers Class 10 Important Questions Very Short Answer (1 Mark)
Question 1.
The decimal expansion of the rational number 43/2453 will terminate after how many places of decimals?
Year of Question:(2013)
Solution:
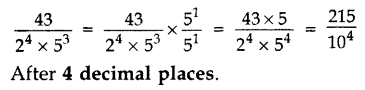
Question 2.
Write the decimal form of 129/275775
Year of Question:(2010)
Solution:
Non-terminating non-repeating.
Question 3.
Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11, and 15 respectively.
Year of Question:(2016)
Solution:
Algorithm
398 - 7 = 391, 436 - 11 = 425, 542 - 15 = 527
HCF of 391, 425, 527 = 17
Question 4.
Express 98 as a product of its primes.
Solution:
2 × 72
Question 5.
If the HCF of 408 and 1032 is expressible in the form 1032 × 2 + 408 × p, then find the value of p.
Year of Question:(2015)
Solution:
HCF of 408 and 1032 is 24.
1032 × 2 + 408 × (p) = 24
408p = 24 - 2064
p = -5
Real Numbers Class 10 Important Questions Short Answer-I (2 Marks)
Question 6.
HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number.
Year of Question:(2012)
Solution:
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 9×459/27 = 153
Question 7.
Find HCF and LCM of 13 and 17 by prime factorisation method.
Year of Question:(2013)
Solution:
13 = 1 × 13; 17 = 1 × 17
HCF = 1 and LCM = 13 × 17 = 221
Question 8.
Find LCM of numbers whose prime factorisation are expressible as 3 × 52 and 32 × 72.
Year of Question:(2014)
Solution:
LCM (3 × 52, 32 × 72) = 32 × 52 × 72 = 9 × 25 × 49 = 11025
Question 9.
Find the LCM of 96 and 360 by using fundamental theorem of arithmetic.
Year of Question:(2012)
Solution:
96 = 25× 3
360 = 23× 32 × 5
LCM = 25× 32 × 5 = 32 × 9 × 5 = 1440
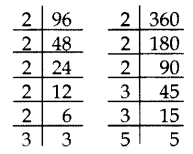
Question 10.
Find the HCF (865, 255) using Euclid’s division lemma.
Year of Question:(2013)
Solution:
865 > 255
865 = 255 × 3 + 100
255 = 100 × 2 + 55
100 = 55 × 1 + 45
55 = 45 × 1 + 10
45 = 10 × 4 + 5
10 = 5 × 2 + 0
The remainder is 0.
HCF = 5

Question 11.
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
Year of Question:(2015)
Solution:
It is given that on dividing 70 by the required number, there is a remainder 5.
This means that 70 - 5 = 65 is exactly divisible by the required number.
Similarly, 125 - 8 = 117 is also exactly divisible by the required number.
65 = 5 × 13
117 = 32 × 13
HCF = 13
Required number = 13
Question 12.
Find the prime factorisation of the denominator of rational number expressed as 6.12¯ in simplest form.
Year of Question:(2014)
Solution:
Let x = 6.12¯ .(i)
100x = 612.12¯ .(ii)
.[Multiplying both sides by 100]
Subtracting (i) from (ii),
99x = 606
x = 60699 = 20233
Denominator = 33
Prime factorisation = 3 × 11
Question 13.
Complete the following factor tree and find the composite number x.
Year of Question:(2014)
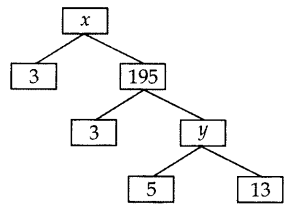
Solution:
y = 5 × 13 = 65
x = 3 × 195 = 585
Question 14.
Prove that 2 + 3√5 is an irrational number.
Year of Question:(2014)
Solution:
Let us assume, to the contrary, that 2 + 3√5 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 2 + 3√5 = ab, where a and b are coprime.
Rearranging the above equation, we get
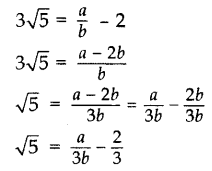
Since a and b are integers, we get a/3b−2/3 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So, we conclude that 2 + 3√5 is irrational.
Question 15.
Show that 3√7 is an irrational number.
Year of Question:(2016)
Solution:
Let us assume, to the contrary, that 3√7 is rational.
That is, we can find coprime a and b (b ≠ 0) such that 3√7 = ab
Rearranging, we get √7 = a/3b
Since 3, a and b are integers, a/3b is rational, and so √7 is rational.
But this contradicts the fact that √7 is irrational.
So, we conclude that 3√7 is irrational.
Question 16.
Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number?
Year of Question:(2015)
Solution:
17 × 5 × 11 × 3 × 2 + 2 × 11 .(i)
= 2 × 11 × (17 × 5 × 3 + 1)
= 2 × 11 × (255 + 1)
= 2 × 11 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.
Question 17.
Check whether 4n can end with the digit 0 for any natural number n.
Year of Question:(2015)
Solution:
4n = (22)n = 22n
The only prime in the factorization of 4n is 2.
There is no other prime in the factorization of 4n = 22n
(By uniqueness of the Fundamental Theorem of Arithmetic).
5 does not occur in the prime factorization of 4nfor any n.
Therefore, 4n does not end with the digit zero for any natural number n.
Question 18.
Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons.
Year of Question:(2017 OD)
Solution:
No, LCM = Product of the highest power of each factor involved in the numbers.
HCF = Product of the smallest power of each common factor.
We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF
We are given that,
LCM = 175 and HCF = 15
175 = k × 15
⇒ 11.67 = k
But in this case, LCM ≠ k × HCF
Therefore, two numbers cannot have LCM as 175 and HCF as 15.
Real Numbers Class 10 Important Questions Short Answer-II (3 Marks)
Question 19.
Prove that √5 is irrational and hence show that 3 + √5 is also irrational.
Year of Question:(2012)
Solution:
Let us assume, to the contrary, that √5 is rational.
So, we can find integers p and q (q ≠ 0), such that
√5 = p/q, where p and q are coprime.
Squaring both sides, we get
5 = p2/q2
⇒ 5q2 = p2 .(i)
⇒ 5 divides p2
5 divides p
So, let p = 5r
Putting the value of p in (i), we get
5q2 = (5r)2
⇒ 5q2 = 25r2
⇒ q2 = 5r2
⇒ 5 divides q2
5 divides q
So, p and q have atleast 5 as a common factor.
But this contradicts the fact that p and q have no common factor.
So, our assumption is wrong, is irrational.
√5 is irrational, 3 is a rational number.
So, we conclude that 3 + √5 is irrational.
Question 20.
Prove that 3 + 2√3 is an irrational number.
Year of Question:(2014)
Solution:
Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = ab, where a and b are coprime.
Rearranging the equations, we get
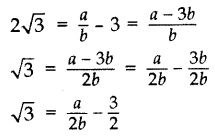
Since a and b are integers, we get a/2b?3/2 is rational and so √3 is rational.
But this contradicts the fact that √3 is irrational.
So we conclude that 3 + 2√3 is irrational.
Question 21.
Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together?
Year of Question:(2013)
Solution:
9 = 32, 12 = 22 × 3, 15 = 3 × 5
LCM = 22 × 32 × 5 = 4 × 9 × 5 = 180 minutes or 3 hours
They will next toll together after 3 hours.
Question 22.
Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times.
Year of Question:(2012)
Solution:
To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 52 × 17
680 = 23 × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.

Question 23.
The length, breadth, and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
Year of Question:(2015)
Solution:
To find the length of the longest rod that can measure the dimensions of the room exactly, we have to find HCF.
L, Length = 8 m 50 cm = 850 cm = 21 × 52 × 17
B, Breadth = 6 m 25 cm = 625 cm = 54
H, Height = 4 m 75 cm = 475 cm = 52 × 19
HCF of L, B and H is 52 = 25 cm
Length of the longest rod = 25 cm
Question 24.
Three alarm clocks ring at intervals of 4, 12 and 20 minutes respectively. If they start ringing together, after how much time will they next ring together?
Year of Question:(2015)
Solution:
To find the time when the clocks will next ring together,
we have to find LCM of 4, 12 and 20 minutes.
4 = 22
12 = 22 × 3
20 = 22 × 5
LCM of 4, 12 and 20 = 22 × 3 × 5 = 60 minutes.
So, the clocks will ring together again after 60 minutes or one hour.
Question 25.
In a school, there are two Sections A and B of class X. There are 48 students in Section A and 60 students in Section B. Determine the least number of books required for the library of the school so that the books can be distributed equally among all students of each Section.
Year of Question:(2017 OD)
Solution:
Since the books are to be distributed equally among the students of Section A and Section B. therefore, the number of books must be a multiple of 48 as well as 60.
Hence, required num¬ber of books is the LCM of 48 and 60.
48 = 2
4 × 3
60 = 2
2 × 3 × 5
LCM = 2
4 × 3 × 5 = 16 × 15 = 240
Hence, required number of books is 240.
Question 26.
By using Euclid’s algorithm, find the largest number which divides 650 and 1170.
Year of Question:(2017 OD)
Solution:
Given numbers are 650 and 1170.
1170 > 650
1170 = 650 × 1 + 520
650 = 520 × 1 + 130
520 = 130 × 4 + 0
HCF = 130
The required largest number is 130.
Question 27.
Find the HCF of 255 and 867 by Euclid’s division algorithm.
Year of Question:(2014)
Solution:
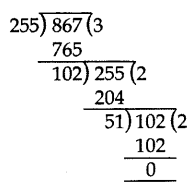
867 is greater than 255. We apply the division lemma to 867 and 255, to get
867 = 255 × 3 + 102
We continue the process till the remainder is zero
255 = 102 × 2 + 51
102 = 51 × 2 + 0, the remainder is zero.
HCF = 51
Question 28.
Using Euclid’s division algorithm, find whether the pair of numbers 847, 2160 are coprime or not.
To find out the minimum (least) time when the bells toll together next, we find the LCM of 9, 12, 15.
Year of Question:(2014)
Solution:

Real Numbers Class 10 Important Questions Long Answer (4 Marks)
Question 29.
Prove that 3 + 2√5 is irrational.
Year of Question:(2012, 2017 D)
Solution:
Let us assume, to the contrary, that 3 + 2√5 is rational
So that we can find integers a and b (b ≠ 0), such that
3 + 2 √5 = a/b, where a and b are coprime.
Rearranging this equation, we get

Since a and b are integers, we get that a/2b - 3/2 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So we conclude that 3 + 2√5 is irrational.
Question 30.
There are 104 students in class X and 96 students in class IX in a school. In a house examination, the students are to be evenly seated in parallel rows such that no two adjacent rows are of the same class.
(a) Find the maximum number of parallel rows of each class for the seating arrange¬ment.
(b) Also, find the number of students of class IX and also of class X in a row.
(c) What is the objective of the school administration behind such an arrangement?
Year of Question:(2013)
Solution:
104 = 23 × 13
96 = 25 × 3
HCF = 23 = 8
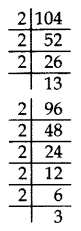
(a) Number of rows of students of class X = 104/8 = 13
Number maximum of rows class IX = 96/8 = 12
Total number of rows = 13 + 12 = 25
(b) No. of students of class IX in a row = 8
No. of students of class X in a row = 8
(c) The objective of school administration behind such an arrangement is fair and clean examination, so that no student can take help from any other student of his/her class.
Question 31.
Dudhnath has two vessels containing 720 ml and 405 ml of milk respectively. Milk from these containers is poured into glasses of equal capacity to their brim. Find the minimum number of glasses that can be filled.
Year of Question:(2014)
Solution:
1st vessel = 720 ml; 2nd vessel = 405 ml
We find the HCF of 720 and 405 to find the maximum quantity of milk to be filled in one glass.
405 = 34 × 5
720 = 24× 32× 5
HCF = 32 × 5 = 45 ml = Capacity of glass
HCF = 32 × 5 = 45 ml = Capacity of glass
No. of glasses filled from 1st vessel = 720/45 = 16
No. of glasses filled from 2nd vessel = 405/45 = 9
Total number of glasses = 25
Question 33.
Find HCF of numbers 134791, 6341 and 6339 by Euclid’s division algorithm.
Year of Question:(2015)
Solution:
First, we find HCF of 6339 and 6341 by Euclid’s division method.
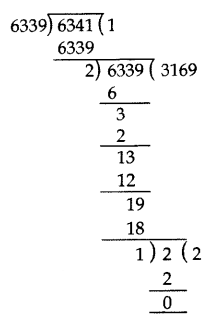
6341 > 6339
6341 = 6339 × 1 + 2
6339 = 2 × 3169 + 1
2 = 1 × 2 + 0
HCF of 6341 and 6339 is 1.
Now, we find the HCF of 134791 and 1
134791 = 1 × 134791 + 0
HCF of 134791 and 1 is 1.
Hence, the HCF of the given three numbers is 1.
Question 34.
If two positive integers x and y are expressible in terms of primes as x = p2q3 and y = p3q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain.
Year of Question:(2014)
Solution:
x = p2q3 and y = p3q
LCM = p3q3
HCF = p2q ...(i)
Now, LCM = p3q3
⇒ LCM = pq2 (p2q)
⇒ LCM = pq2 (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 22 × 3
b = 18 = 2 × 32
HCF = 2 × 3 = 6 .(ii)
LCM = 22 × 32 = 36
LCM = 6 × 6
LCM = 6 (HCF) .[From (ii)]
Here LCM is 6 times HCF.
Question 35.
Show that one and only one out of n, (n + 1) and (n + 2) is divisible by 3, where n is any positive integer.
Year of Question:(2015)
Solution:
Let n, n + 1, n + 2 be three consecutive positive integers.
We know that n is of the form 3q, 3q + 1, or 3q + 2.
Case I. When n = 3q,
In this case, n is divisible by 3,
but n + 1 and n + 2 are not divisible by 3.
Case II. When n = 3q + 1,
In this case n + 2 = (3q + 1) + 2
= 3q + 3
= 3(q + 1 ), (n + 2) is divisible by 3,
but n and n + 1 are not divisible by 3.
Case III.
When n = 3q + 2, in this case,
n + 1 = (3q + 2) + 1
= 3q + 3 = 3 (q + 1 ), (n + 1) is divisible by 3,
but n and n + 2 are not divisible by 3.
Hence, one and only one out of n, n + 1 and n + 2 is divisible by 3.
Question 36.
Find the HCF and LCM of 306 and 657 and verify that LCM × HCF = Product of the two numbers.
Year of Question:(2016 D)
Solution:
306 = 2 × 32 × 17
657 = 32 × 73
HCF = 32 = 9
LCM = 2 × 32 × 17 × 73 = 22338
L.H.S. = LCM × HCF = 22338 × 9 = 201042
R.H.S. = Product of two numbers = 306 × 657 = 201042
L.H.S. = R.H.S.
Question 37.
Show that any positive odd integer is of the form 41 + 1 or 4q + 3 where q is a positive integer.
Year of Question:(2016 D)
Solution:
Let a be a positive odd integer
By Euclid’s Division algorithm:
a = 4q + r .[where q, r are positive integers and 0 ≤ r < 4]
a = 4q
or 4q + 1
or 4q + 2
or 4q + 3
But 4q and 4q + 2 are both even
a is of the form 4q + 1 or 4q + 3.
Important Questions & Answers on Real Numbers
Question 1.
What is the Fundamental Theorem of Arithmetic?
Answer:
Definition:
Every composite number can be expressed as a unique product of "prime numbers" (excluding the order of factors).
Example:
The number 60 can be factorized as 60=2×2×3×5=2²×3×5.
This prime factorization is unique for 60, apart from the order.
Question 2.
Explain Euclid’s Division Algorithm and how it’s used to find the HCF.
Answer:
Definition:
For any two integers a and b (where a > b a > b), Euclid’s Division Algorithm states:
a = bq + r, where r < b
r<b and q is the quotient, r is the remainder.
If r - 0, then b is the HCF of a and b.
Steps to Find HCF Using Euclid’s Algorithm:
Step 1: Divide the larger number by the smaller number.
Step 2: Take the remainder and divide the previous divisor by this remainder.
Step 3: Repeat until the remainder is 0; the last divisor is the HCF.
Question 3.
How do you find the HCF and LCM of two numbers using Prime Factorization?
Answer:
HCF Calculation:
Factorize each number into primes.
Take the smallest power of each common prime factor.
Multiply these to get the HCF.
LCM Calculation:
Take the highest power of all prime factors found in both numbers.
Multiply these to get the LCM.
Example:
For 6 and 20:
Prime factors of 6:2×3
Prime factors of 20: 2×2×5=2²×5
HCF: 2 (smallest power of 2)
LCF: 2²×3×5-60
Question 4.
Prove that √2 is an irrational number.
Answer:
Proof by Contradiction:
Assume √2 is rational, so it can be written as a/b where a and b are coprime (have no common factors other than 1).
Step 1: √2 a/b
Step 2: Squaring both sides gives 2a² - a², So a² is even, making a even.
Step 3: Let a-2c Substitute a-2c back, giving b²-2c² making b also even.
Contradiction: a and b cannot both be even if they are coprime, so √2 is irrational
Question 5.
What is the difference between rational and irrational numbers?
Answer:
Rational Numbers:
Can be expressed as a fraction p/q where p and q are integers and q≠0
Examples: 1/2 ?3,0.75
Irrational Numbers:
Cannot be expressed as a fraction of two integers.
Examples include √2 √3 π
Question 6.
How does the Fundamental Theorem of Arithmetic help in determining the type of decimal expansion for a rational number?
Answer:
Terminating Decimal:
A rational number has a terminating decimal expansion if the prime factors of its denominator (after simplification) are only 2 or 5.
Non-Terminating Repeating Decimal:
If the denominator has prime factors other than 2 or 5, the decimal expansion is non-terminating repeating.
Example:
7/8-0.875(terminates because the denominator, 8, factors as 23).
1/3-0.333...(repeats because 3 is a prime factor other than 2 or 5).
Question 7.
Why can’t 4nend with the digit zero for any natural number n?
Answer:
Reason:
A number ending in zero must be divisible by 5.
4^n (where 4n-(2)² n) only has 2 as its prime factor.
Since 5 is not a factor of 4^n, it cannot end in zero.
Question 8.
Explain why 5×7×11+7 is a composite number.
Answer:
Definition of Composite Number:
A composite number has more than two factors.
Explanation:
5×7×11+7 can be factored as 7(5×11+1) -7 × 56.
Since 7 and 56
56 are factors of this expression, it has more than two factors, so it’s a composite number.
Question 9.
How can we use the Fundamental Theorem of Arithmetic to find the LCM of three numbers?
Answer:
Steps to Find LCM of Three Numbers (e.g., 6, 72, 120):
Prime factorize each number.
6:2 × 3
72:23× 3²
120:23× 3 × 5
Take the highest powers of all primes present:
23, 3², and 5
Multiply these: LCM - 23× 3² × 5 - 360