Question 1.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Given: the ratio of the angles of quadrilateral are 3 : 5 : 9 : 13.
Let the angles of the quadrilateral are 3x, 5x, 9x and 13x.
We know that, sum of angles of a quadrilateral = 360°
∴ 3x + 5x+ 9x+13x = 360°
⇒ 30x = 360° ⇒ x = 360°/30 = 12°
∴ Angles of the quadrilateral are 3x = 3 x 12 = 36°
5x = 5 x 12 = 60°
9x= 9×12 = 108°
and 13x = 13×12 = 156°
Question 2.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Let given parallelogram is ABCD whose diagonals AC and BD are equal, i.e., AC = BD.
Now, we have to prove that ABCD is a rectangle.
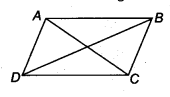
Proof: In ∆ ABC and ∆ DCB, we have
AB = CD (Opposite sides of parallelogram)
BC = CB (Common in both triangles)
and AC = BD (Given)
∴ ∆ABC ≅ ∆DCB (By SSS rule)
∴ ∆ABC = ∠DCB .(i)
(Corresponding Part of Congruent Triangle)
But DC || AB and transversal CB intersect them.
∴ ∠ABC+ ∠DCB = 180°
(∵ Both are interior angles on the same side of the transversal)
⇒ ∠ABC + ∠ABC = 180° [From Eq. (i)]
⇒ 2 ∠ABC = 180°
⇒ ∠ABC = 90°= ∠DCB
Thus, ABCD is a parallelogram and one of angles is 90°.
Hence, ABCD is a rectangle.
Hence proved.
Question 3.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Given: a quadrilateral ABCD whose diagonals AC and BD bisect each other at right angles.
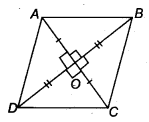

Hence, from Eqs. (i), (ii) and (iii), we get
AB = BC = AD = CD
Hence, ABCD is a rhombus.
Hence proved.
Question 4.
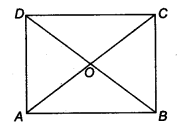
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given: A square ABCD whose diagonals AC and BD intersect at O.
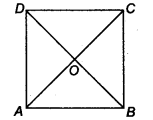


Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
Given: A quadrilateral ABCD in which AC = BD and AC ⊥ BD such that OA = OC and OB = OD. So, ABCD is a parallelogram.
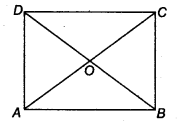
To prove: ABCD is a square.
Proof: Let AC and BD intersect at a point O.
In ∆ABO and ∆ADO, we have
BO = OD (Given)
AO = OA (Common)
∠AOB = ∠AOD = 90° (Given)

Question 6.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
- (i) it bisects ∠C also,
- (ii) ABCD is a rhombus.
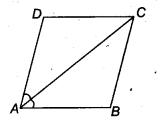
Solution:
Given: diagonal AC of a parallelogram ABCD bisects ∠A
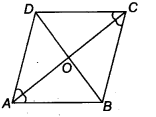

Hence, ABCD is a rhombus.
Hence proved.
Question 7.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well AS ∠D.
Solution:
Given: ABCD is a rhombus

∴ AD = AB = BC = CD ..(i)
To prove:
(i) Diagonal AC bisect ∠A as well as ∠C.
(ii) Diagonal BD bisects ∠B as well as ∠D.
Proof:
(i) Let AC and BD are the diagonals of rhombus ABCD.
In ∆ABC and ∆ADC,
AD = AB
CD = BC [From Eq,(i)]
and AC = CA (Common)

Question 8.
ABCD is a rectangle in which diagonal AC bisects ?A as well as ?C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ? B as well as ?D.
Solution:
Given: ABCD is a rectangle.


Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that
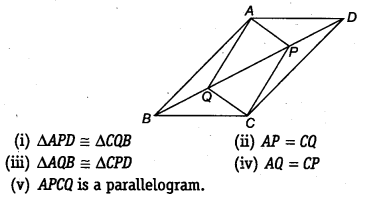
Solution:
Given: ABCD is a parallelogram and P and Q are lie on BD such that



Question 10.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see figure). Show that
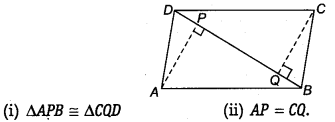



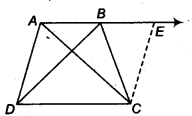


Hence Proved
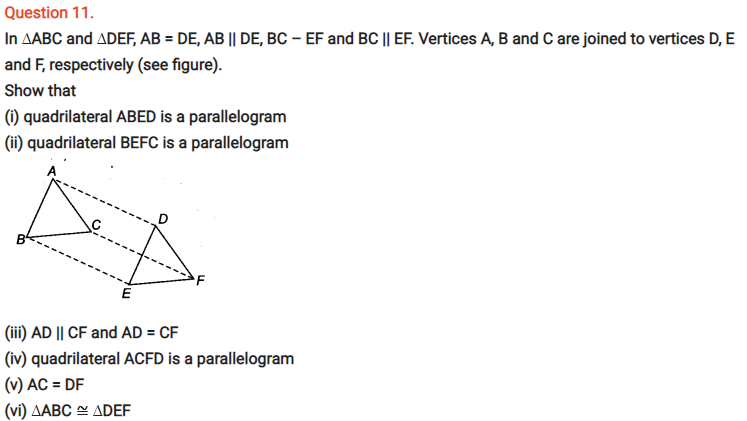
Question 1.
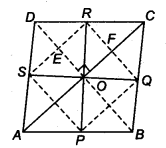
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that
- (i) SR || AC and SR = 1/2 AC
- (ii) PQ = SR
- (iii) PQRS is a parallelogram.
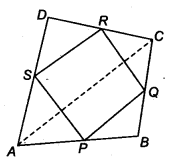
Solution:
Given: P, Q, Ft and S are mid-points of the sides.
∴ AP = PB, BQ = CQ
CR = DR and AS = DS
(i) In ∆ADC, we have
S is mid-point of AD and R is mid-point of the DC.
We know that, the line segment joining the mid-points of two sides of a triangle is parallel to the third side.

Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA
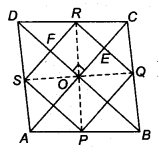
By mid-point theorem,

∴ PQRS is a parallelogram.
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF = 90°
Now, RQ || BD (By mid-point theorem)
⇒ RE || OF
Also, SP|| AC [From Eq. (i)]
⇒ FR || OE
∴ OERF is a parallelogram.
So, ∠ ERF = ∠EOF = 90°
(Opposite angle of a quadrilateral is equal)
Thus, PQRS is a parallelogram with ∠R = 90°
Hence, PQRS is a rectangle.
Question 3.
ABCD is a rectangle and P, Q, R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: ABCD is a rectangle.
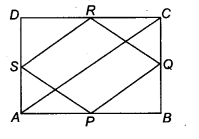
∴ ∠A = ∠B = ∠C= ∠D = 90°
and AD = BC, AB = CD

Question 4.
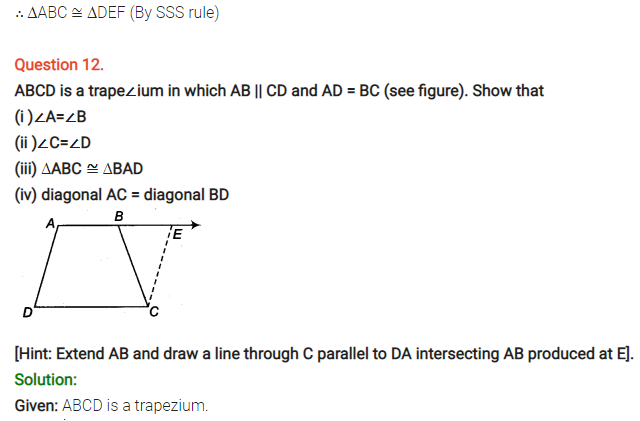
ABCD is a trapezium in which AB | | DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
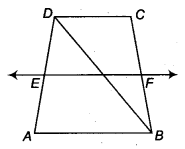
Solution:
Given: ABCD is a trapezium in which AB || CD and E is mid-point of AD and EF || AB.
In ∆ABD, we have
EPAB
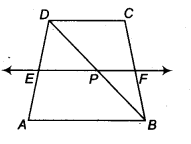
and E is mid-point of AD.
So, by theorem, if a line drawn through the mid-point of one side of a triangle parallel to another side bisect the third side.
∴ P is mid-point of BD.
Similarly, in ∆ BCD, we have,
PF || CD (Given)
and P is mid-point of BD.
So, by converse of mid-point theorem, F is mid-point of CB.
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
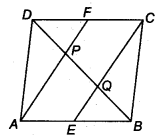

BQ = PQ = PD
Hence, CE and AF trisect the diagonal BD.
Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Let ABCD is a quadrilateral and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively, i.e., AS = SD, AP = BP, BQ = CQ and CR = DR. We have to show that PR and SQ bisect each other i.e., SO = OQ and PO = OR.